纵观生成式AI领域中的两个主导者:自回归和扩散模型。
一个专攻文本等离散数据,一个长于图像等连续数据。
如果,我们让后者来挑战前者的主场,它能行吗?
斯坦福博士的最新研究,就搞了这么一个扩散模型VS自回归模的同台PK。
结果:
挑战成功!(下面为生成示意图,最后得到的文本是“Hello world,I am a language diffusion model,named SEDD”)

并且他们的扩散模型在困惑度和质量上已率先超越自回归的GPT-2。

赶紧来瞧瞧。
01 扩散模型挑战离散数据
用自回归来处理离散文本数据,即根据之前的token来预测下一个token,这可能是目前我们能想象到的最简单可行的方法。
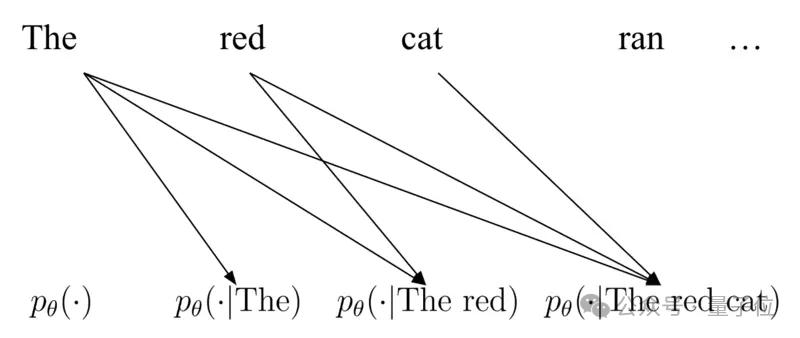
为什么这么说?
作者在这里用GAN举了个例子:
对于图像生成,GAN首先根据随机噪声生成图像,然后使用判别器来“惩罚”偏差,因此梯度信息可以反向传播到生成器。

但如果我们假设用GAN来生成文本,就行不通了。
因为尽管我们可以定义同样原理的生成器和判别器,但文本的离散性质使得更新生成器非常难。
(图像是连续的,因此可以通过反向传播来计算梯度,但文本是一堆无法区分的离散值,计算梯度信号相当繁琐,基本只能粗略估计)

所以说,文本建模领域基本成了自回归的天下(如transformer的发扬光大就是基于自回归模型)。
不过,这个架构也有根本性的缺陷:
最有名的“批评”来自Lecun,他就认为自回归transformer“注定要失败”,因为生成会“偏离”数据分布并导致模型在采样过程中发散。
除此之外,自回归架构的采样也具有高度迭代性,这对为并行计算而高度优化的GPU来说也不够match。
最后,由于这类架构的模型都是按照从左往右地完成任务,因此一次执行多个控制任务也很困难(例如补充给定了前缀和后缀的文本)。
正是这些缺点促使作者开始构思另一种概率模型,因此有了本文的主角:
分数熵离散扩散模型(SEDD,Score Entropy Discrete Diffusion)。
简单来说,为了将扩散模型扩展到离散空间,就必须将“分数函数”(也就是对数概率的梯度)概念推广到离散空间。
幸运的是,有一种替代方案可以呈现具体分数,即概率的局部比率。
如下图所示,左边为分数函数,它直观地“指向”连续空间中的较高密度区域,具体分数(右)将其推广到离散空间。
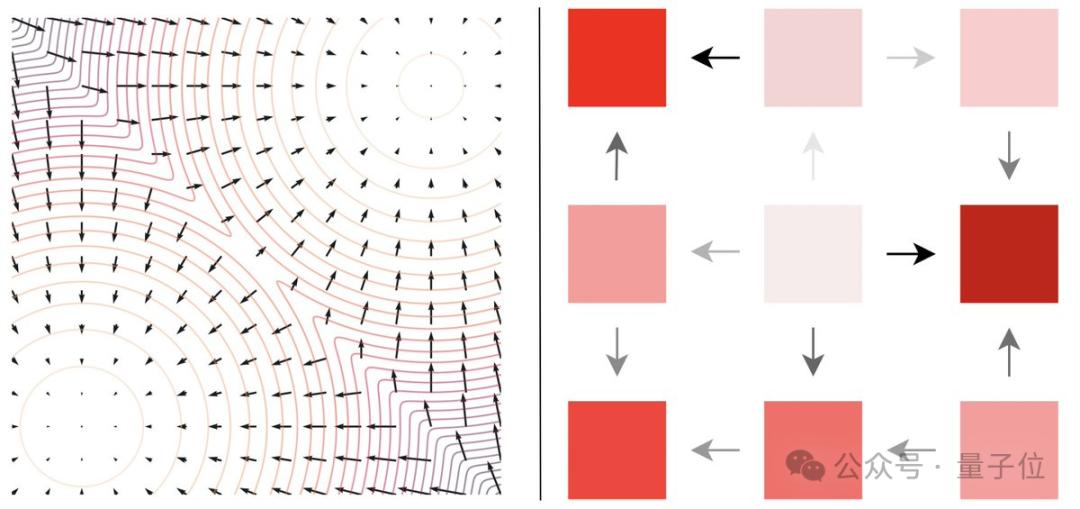
这些具体的比率(分数)可以通过得分熵(score entropy)损失函数来学习,从而实现离散扩散模型的快速、可扩展训练。
在这之中,由于作者只知道可以使用得分熵从数据中学习具体得分(对应于学习概率模型),但仍然不知道如何生成样本。
因此还借用了扩散模型的核心思想,并使用学习到的具体分数将随机值迭代地去噪为数据点。
为此,他们还定义了向离散文本样本中“添加噪声”的含义:
对于连续空间,这是通过添加高斯噪声自然产生的,但在离散空间中,则是被迫直接在不同元素之间“跳跃”。

而最终,他们的SEDD模型通过学习将样本不断迭代去噪为文本,完成从纯随机输入生成文本的任务。
02 超越GPT-2
总的来看,与自回归模型相比,该扩散模型可以在生成过程中利用完整的全局上下文,从而获得更好的整体生成效果。
对比起来,自回归模型特别是像GPT-2这样的会发生“漂移”现象,从而破坏整体性能的稳定性。
并且即使在较小的模型规模下,SEDD也能始终生成高质量的文本(绿框,读者很通顺),而GPT-2就比较困难(红框,一眼看上去就很多错误)。

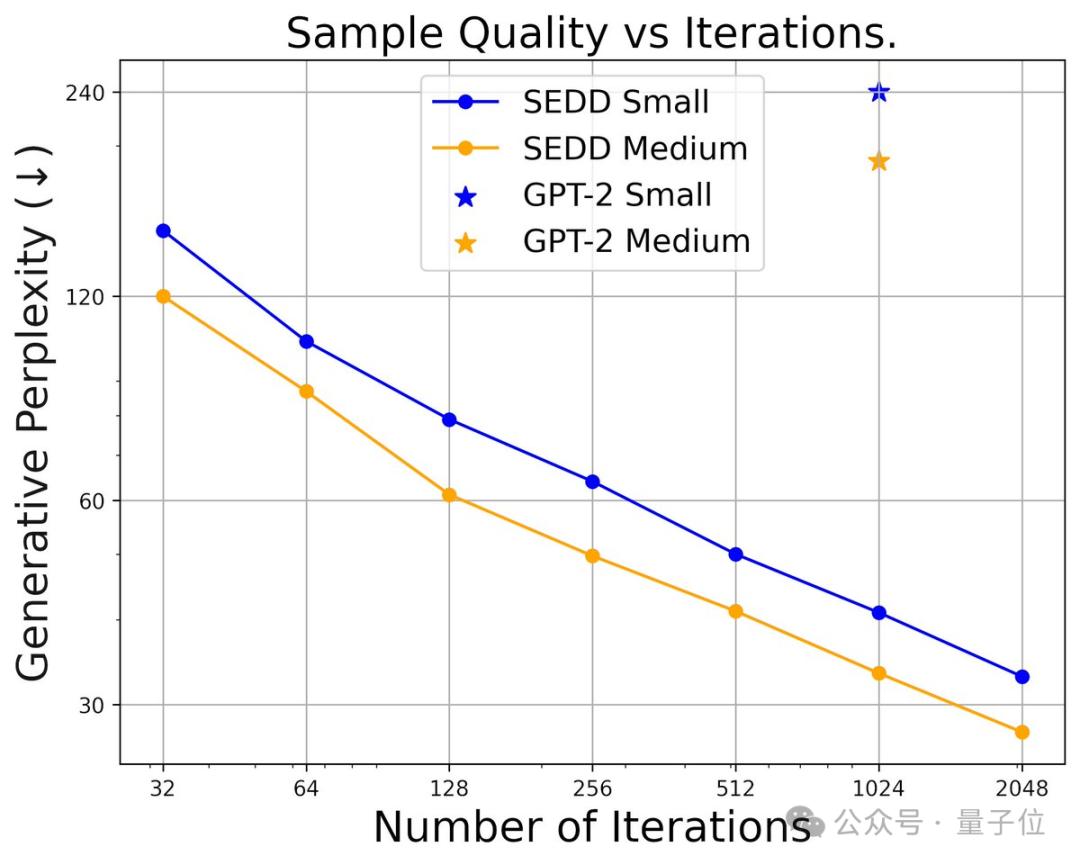
具体测试中,SEDD在困惑度指标上表现出了很强的竞争力:
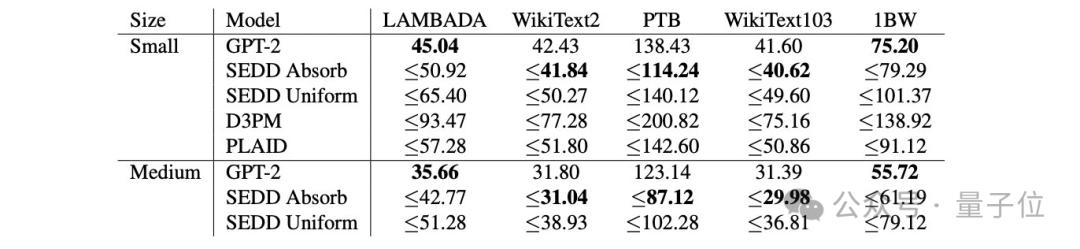
此外,作者还发现:
使用更少的采样步骤,SEDD照样在控制生成质量上的表现也比GPT-2要好。
最后,团队以完全零样本的方式从任意位置提示SEDD后发现:对于标准(从左到右)和非标准(填充)提示方法,SEDD都可以与最好的GPT-2解码方法一较高下。
如下图所示:
提示标记以蓝色表示,不管它在前面中间还是结尾,SEDD都能够生成有意义的文本。

03 Pika创始人是作者之一
本研究一共3位作者:

一作为斯坦福计算机专业博士生Aaron Lou,康奈尔本科毕业。
二作也是该校博士生Chenlin Meng。
她的名字不算陌生,Pika就是她(下图右)和“学妹”郭文景一起创办的。(Meng 2020年入学斯坦福,郭2021年入学)
看起来,一边创业的她也一边兼顾着学业。

最后,通讯作者为一二作的导师Stefano Ermon,他是斯坦福计算机科学系副教授。




 首页
首页
 AI对话
AI对话
 资讯
资讯  我的
我的